Public-key cryptography is a technique that allows communication between parties without having to exchange secret keys. Before public-key cryptography, the two parties would physically exchange an encryption/decryption key to maintain secure communications. Encrypted communications and digital signatures use public-key encryption. Blockchains and decentralized networks use digital signatures to prove ownership of addresses.
I also created a math and code tutorial.
How Public-Key Cryptography Works
First, we will cover the precursors to public-key cryptography.
Basic Ciphers
Ciphers have coded messages for thousands of years. A cipher is an algorithm that alters a message to make reading it difficult. The sender and recipient must know the cipher. A famous example is the Caesar Cipher. The Caesar Cipher shifts each letter by three places, seen below:
normal alphabet a b c d e f g h i j k l m n o p q r s t u v w x y z
cipher alphabet d e f g h i j k l m n o p q r s t u v w x y z a b c
"HELLO" would be encoded as "KHOOR."
Simple ciphers are easy to use. Computers can easily compromise simple ciphers. As a result, they have fallen out of favor.
Symmetric-Key Cryptography
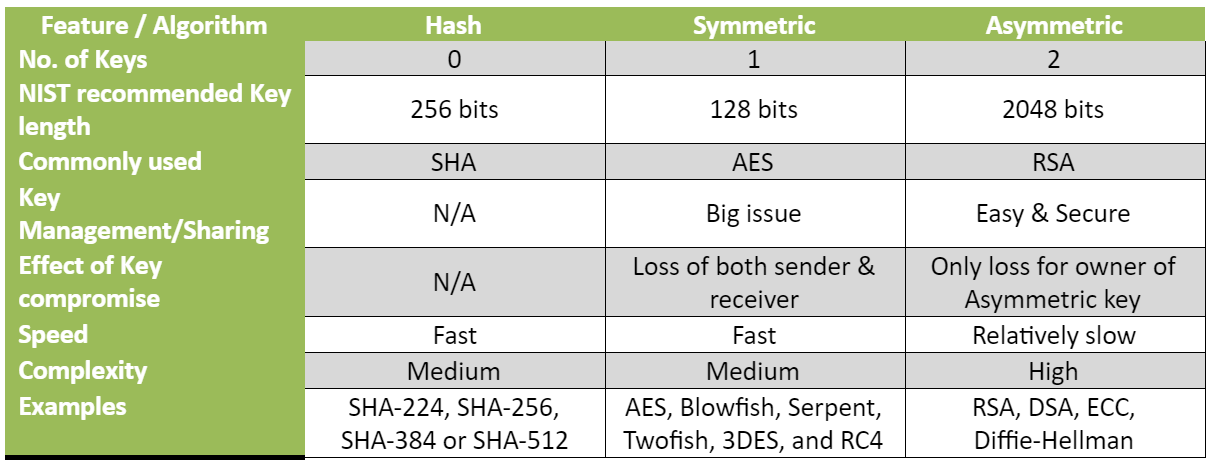
Symmetric-key cryptography is a more advanced cipher. A respected algorithm like the Advanced Encryption Standard (AES) is still a substitution cipher. A "key" is used to instruct the encryption algorithm on how to do substitutions. AES uses a 128-bit key.
Example Key:
54 68 61 74 73 20 6D 79 20 4B 75 6E 67 20 46 75
Instead of one substitution like the Caesar Cipher, AES goes through many rounds. The 128-bit key generates sub-keys for each substitution round. The sub-keys ensure a different substitution algorithm is used for each round. The computer processing time needed to break the encryption is impractical.
Symmetric-key cryptography has the challenge of exchanging keys between parties without the keys being lost or intercepted. Public-key cryptography allows symmetric keys to be encrypted and safely transmitted over insecure channels. Symmetric-key algorithms are much faster than public-key algorithms. It is a common practice to share symmetric keys through public-key encryption for further communication using symmetric keys.
Public-Key Cryptography
Public-key cryptography or asymmetric cryptography is a security advance on ciphers. Each participant has a public key and a private key. The public key is shared openly without compromising security. Messages are encrypted using the recipient's public key. Only the recpient's private key can decrypt the message. Users can send messages over insecure channels without interception. A user can send an encrypted message to a wide range of participants without previously knowing them or meeting to exchange keys.
This public key and private key pairing are possible through the use of asymmetric math. Asymmetric math uses one-way functions. Using a private key to decrypt a message encrypted with the associated public key is easy. It is nearly impossible to do the opposite and find the private key given only the public key. The most popular public-key schemes, such as RSA, use unique properties of prime numbers to create these one-way functions. Multiplying large prime numbers together to find a product and creating keys from the product is fast. Deducing the original primes from the product is tortuous.
The math and code tutorial covers creating keys, encrypting a message, then decrypting it. The example covers the basic math process used for algorithms like RSA.
 Source: Cryptomathic.com
Source: Cryptomathic.com
Applications
Encryption
Encrypting messages without exchanging a secret key is a use case for pubic-key cryptography. Given the size and anonymity of decentralized networks, the ability to communicate with users without meeting to exchange keys is critical.
Digital Signatures
There are many definitions for digital signatures. I define digital signature as using public-key cryptography to prove that an owner of a set of keys authored a message or transaction.
One of the most common methods for digital signatures uses RSA-created keys. The signer computes the hash value of the message and encodes it with their private key. Any recipient of the message can use the sender's public key to validate the signature.
Bitcoin and other blockchains use digital signatures to authorize transactions.
If this simplistic explanation is lacking and you have questions like "Won't this expose the signers private key to everyone?" Please check the math and code tutorial for a more in-depth explanation of how the math works behind digital signatures.
Authentication
A variation of digital signatures can authenticate users. You register for an account using your public key as a username. Log in by sending the service a digital signature confirming you are the owner (or at least in possession of the private key) for the username/public key. The service logs you in.
Applications on the Ethereum Blockchain use this method. Logging in takes one click in your wallet's browser popup.
Secure log-in to remote servers uses a protocol based on digital signatures.
Further Reading
Public-Key Cryptography Math and Code Tutorial.
Read my post on hash functions to understand another important concept in blockchains and decentralized networks.
Hash Function Coding Tutorial to learn concepts hands-on.
Bitcoin White Paper
Understanding Public-Key Cryptography
2021 June 15 Twitter Substack See all postsIt is difficult to read any technical literature on blockchains or decentralized networks without understanding public-key cryptography.
Public-key cryptography is a technique that allows communication between parties without having to exchange secret keys. Before public-key cryptography, the two parties would physically exchange an encryption/decryption key to maintain secure communications. Encrypted communications and digital signatures use public-key encryption. Blockchains and decentralized networks use digital signatures to prove ownership of addresses.
I also created a math and code tutorial.
How Public-Key Cryptography Works
First, we will cover the precursors to public-key cryptography.
Basic Ciphers
Ciphers have coded messages for thousands of years. A cipher is an algorithm that alters a message to make reading it difficult. The sender and recipient must know the cipher. A famous example is the Caesar Cipher. The Caesar Cipher shifts each letter by three places, seen below:
"HELLO" would be encoded as "KHOOR."
Simple ciphers are easy to use. Computers can easily compromise simple ciphers. As a result, they have fallen out of favor.
Symmetric-Key Cryptography
Symmetric-key cryptography is a more advanced cipher. A respected algorithm like the Advanced Encryption Standard (AES) is still a substitution cipher. A "key" is used to instruct the encryption algorithm on how to do substitutions. AES uses a 128-bit key.
Example Key:
Instead of one substitution like the Caesar Cipher, AES goes through many rounds. The 128-bit key generates sub-keys for each substitution round. The sub-keys ensure a different substitution algorithm is used for each round. The computer processing time needed to break the encryption is impractical.
Symmetric-key cryptography has the challenge of exchanging keys between parties without the keys being lost or intercepted. Public-key cryptography allows symmetric keys to be encrypted and safely transmitted over insecure channels. Symmetric-key algorithms are much faster than public-key algorithms. It is a common practice to share symmetric keys through public-key encryption for further communication using symmetric keys.
Public-Key Cryptography
Public-key cryptography or asymmetric cryptography is a security advance on ciphers. Each participant has a public key and a private key. The public key is shared openly without compromising security. Messages are encrypted using the recipient's public key. Only the recpient's private key can decrypt the message. Users can send messages over insecure channels without interception. A user can send an encrypted message to a wide range of participants without previously knowing them or meeting to exchange keys.
This public key and private key pairing are possible through the use of asymmetric math. Asymmetric math uses one-way functions. Using a private key to decrypt a message encrypted with the associated public key is easy. It is nearly impossible to do the opposite and find the private key given only the public key. The most popular public-key schemes, such as RSA, use unique properties of prime numbers to create these one-way functions. Multiplying large prime numbers together to find a product and creating keys from the product is fast. Deducing the original primes from the product is tortuous.
The math and code tutorial covers creating keys, encrypting a message, then decrypting it. The example covers the basic math process used for algorithms like RSA.
Applications
Encryption
Encrypting messages without exchanging a secret key is a use case for pubic-key cryptography. Given the size and anonymity of decentralized networks, the ability to communicate with users without meeting to exchange keys is critical.
Digital Signatures
There are many definitions for digital signatures. I define digital signature as using public-key cryptography to prove that an owner of a set of keys authored a message or transaction.
One of the most common methods for digital signatures uses RSA-created keys. The signer computes the hash value of the message and encodes it with their private key. Any recipient of the message can use the sender's public key to validate the signature.
Bitcoin and other blockchains use digital signatures to authorize transactions.
If this simplistic explanation is lacking and you have questions like "Won't this expose the signers private key to everyone?" Please check the math and code tutorial for a more in-depth explanation of how the math works behind digital signatures.
Authentication
A variation of digital signatures can authenticate users. You register for an account using your public key as a username. Log in by sending the service a digital signature confirming you are the owner (or at least in possession of the private key) for the username/public key. The service logs you in.
Applications on the Ethereum Blockchain use this method. Logging in takes one click in your wallet's browser popup.
Secure log-in to remote servers uses a protocol based on digital signatures.
Further Reading
Public-Key Cryptography Math and Code Tutorial.
Read my post on hash functions to understand another important concept in blockchains and decentralized networks.
Hash Function Coding Tutorial to learn concepts hands-on.
Bitcoin White Paper